PRACTICA: TRADUCCION: ROTATION, TORQUES

Rotational kinetic energy

Let us picture a rigid body turning with angular velocity ω, like the Earth in this picture. Mentally,

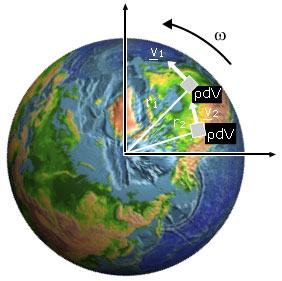let's divide it up into a collection of small masses. With respect to the axis of rotation, a single mass m at radius r is travelling at speed of 

                v = rω
 (You may revise circular motion at this point.) Its kinetic energy is ½ mv². So let's imagine the dividing the object up into many masses m_i at distances r_ifrom the axis. Each has v_i = r_iω, where ω has the same value for all the masses because the object is (by assumption) rigid. So the total rotational kinetic energy is

K_rot= Σ K_i= Σ ½ m_ir_i²ω²

where the summation is over all of the i. ½ ω² is a common factor in every term of the sum, so

K_rot= ½(Σ m_ir_i²)ω² = ½ Iω² where

I = Σ m_ir_i²is the moment of inertia.  

This is the result for a collection of discrete masses, m_i. For a continuous body, we should normally divide it up into small elements of volume, dV. (You can revise calculus.) From the definition of density ρ, each has mass

dm = ρdV.

Instead of an ordinary summation, we do an integral (the equivalent of summation for very small divisions), and we have

K_rot = ½(∫ dm.r²)ω² = ½ Iω² where

I = ∫ r².dm is the moment of inertia for a continous body

and where the integration is over the whole volume occupied by the rigid body in question.

 Rotational kinematics

As mentioned in the multimedia tutorial, there are very strong analogies between linear and rotational kinematics. If s is the distance of the arc travelled along a circle of radius r, then angular displacement θ is just s/r. Angular velocity ω = dθ/dt = (ds/dt)/r = v/r. Angular acceleration α = dω/dt = (dv/dt)/r = a/r.

So, as shown in the diagram below, the analogies of the linear quantities s, v and a are θ, ω and α, which we obtain by dividing the linear quantities by r.

The graphs above show displacement, velocity and acceleration for linear motion with constant acceleration (at left) and for circular motion with constant angular acceleration. Just for practice, let's derive the new equations (and revise the kinematics section if this looks difficult!) If we consider motion with constant acceleration, and remember that α = dω/dt, we have

ω = ∫ α dt = αt + ω₀

And from ω = dθ/dt, we can integrate again to get:

θ = ∫ ω dt = ½αt² + ωt + θ₀

From the two equations above, we can eliminate t to get

ω² − ω₀² = 2α(θ − θ₀).

So we have equations completely analogous to those of linear kinematics:

ω = ω₀ + αt and θ = θ₀ + ω₀t + ½αt² and ω² − ω₀² = 2α(θ − θ₀)
v = v₀ + at and s = s₀ + v₀t + ½at² and v² − v₀² = 2a(s − s₀).

Torque: dependence on displacement, force and angle

Forces cause accelerations. To make something turn, we apply a torque. We shall define if first, and then explain why this definition is logical. Later we shall see the complete analogy with Newton's laws for linear motion.

The torque τ is defined by

τ = rX F

where force F acts at a point displaced by r from the axis. The magnitude of the torque is given by

τ = r F sin θ

where θ is the angle between r and F.

(You may need to look at the cross product section of the  support page on vectors.)

We shall discuss the magnitude first, then the direction.

The photos at right show three ways of using a spanner. In the first pair, we compare a small value of r (small torque) with a large r and large τ. In the second, we compare θ = zero and θ = 90°. In the former case, the torque is zero. From experience, you know that you need large r, θ = 90° and large F to obtain the maximum torque.

                                       Disponible en: http://www.animations.physics.unsw.edu.au/jw/rotation.htm